7.2.6

Summary:

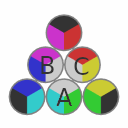
This puzzle consists of 6 pieces,with
3 points to click, namely A, B and C.

Each click rotates 5 of 6 pieces along a semicircular orbit.
Pieces are rotated by 60° or translated, according to the
position and the direction.

After 5 twists, pieces are at their
original places but twisted by 180°.

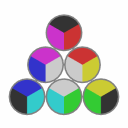→ [A5] →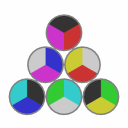

Solved states:

There are these 3 solved states.

Mathematical facts:

· The permutation group of pieces is A6.
· Any piece can be at any of 6 places, and can be twisted by (n×60°).
· The sum of twists is always (n×180°).
So the total number of possible scrambles is: (6!)/2 × (6^6)/3 = 5,598,720.

Solution:

One of methods (maybe not the best) is consisting of 3 steps.
1.Eliminate odd twists(0~2 moves).
2.Eliminate any twists(0~5 moves).
3.Permute pieces preserving twists(0~7 moves).
In total, this requires at most 14 moves.

Example:

Let's solve this scramble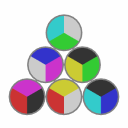

1.Eliminate odd twists
In the above scramble,some pieces have ⅄-shape color borders.
This first step fixes this so that all pieces have Y-shape color borders.
The permutation of pieces doesn't matter at this stage.

→ [B1,A4] →

2.Eliminate any twists
Make so that all corners and centers are white or black.
The permutation still doesn't matter.

→ [A3,B7,C9,B5] →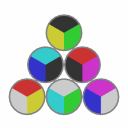

3.Permute pieces preserving twists
This final stage fixes the permutation.
There are 3 sequences, each corresponding to one of 3 solved states.

→ [C1,A4,C8,A1,C9,A5] →

→ [C9,A2,B3,A8,C4,A6] →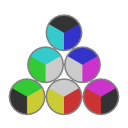

→ [A1,B3,A2,B3,A9,B2,A8]→

The first two are the shortest. So the shortest combined sequences are:
[B1,A7,B7,C9,B5,C1,A4,C8,A1,C9,A5] (11 moves)
and
[B1,A7,B7,C9,B5,C9,A2,B3,A8,C4,A6] (11 moves)