namely A,B and C.
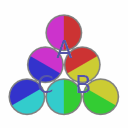
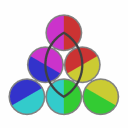
|
After 4 click, pieces are at their original places but twisted by 120°. |
 |
→ [A4] → |  |
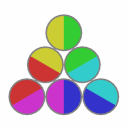
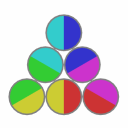
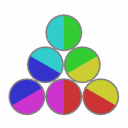
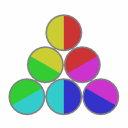
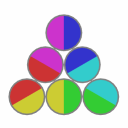
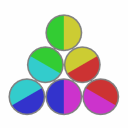
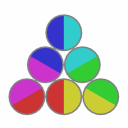
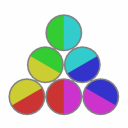
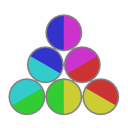
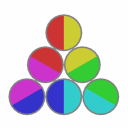
Solved states:
This puzzle has 12 solved states.

| 
| 
| 
| 
| 
|
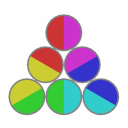
| 
| 
| 
| 
| 
|
Mathematical properties:
· The permutation group of pieces is the transitive subgroup of S6.
· Any piece can be at any of 6 places, and can be twisted by N×60°.
· The sum of twists of pieces by 60° is always even.
Therefore, the total number of possible scrambles is (5!)×(66)÷2=2,799,360.
Solution:
This puzzle can be solved within 7 moves, if a succession of clicks on the same axis is counted 1,
and within 42, otherwise. My solution consists of following two steps.
1. Fix the permutation:
Fix the permutation to one of above solutions(orientation of pieces dosen't matter). This is quite easy. You have 1 in 10 chance that it's already done. And if not, you only need 1 move (since the permutation group is the transitive subgroup of S6, when corner pieces are fixed, the rest is fixed too).
2. Fix the orientation of pieces:
Fix the orientation of pieces preserving relative positions of each pieces. There are only (66)÷2=23,328 patterns. You can find easily within 6 moves sequences for each, by a computer progrram.